622 lines
20 KiB
Markdown
622 lines
20 KiB
Markdown
# C++ STL源码剖析之红黑树
|
||
|
||
## 0.导语
|
||
|
||
在STL源码中有两段话,简单翻译后如下:
|
||
|
||
STL中Red-black tree(红黑树)class,用来当做SLT关系式容器(如set,multiset,map,
|
||
multimap).里面所用的insertion和deletion方法以
|
||
《Introduction to Algorithms》一书为基础,但是有以下两点不同:
|
||
|
||
(1)header不仅指向root,也指向红黑树的最左节点,以便用常数时间实现begin(),并且也指向红黑树的最右边节点,以便
|
||
set相关泛型算法(如set_union等等)可以有线性时间表现.
|
||
|
||
(2)当要删除的节点有两个子节点时,其后继节点连接到其位置,而不是被复制,因此,唯一使无效的迭代器是引用已删除节点的迭代器。
|
||
|
||
上述话翻译成图,如下,相比于普通的红黑树多了一个header节点,并且为红色。普通的红黑树是以100节点开始的,且满足下面五条性质:
|
||
- 每个节点或是红色的,或是黑色的.
|
||
- 根节点是黑色的.
|
||
- 每个叶节点(NULL)是黑色的.
|
||
- 如果一个节点是红色的,则它的两个孩子节点都是黑色的.
|
||
- 对每个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点.
|
||
|
||
当然这里的rb_tree也是一样满足这几条性质,迭代器的begin指向红黑树根节点,也就是header的父亲,而end指向header节点。
|
||
|
||
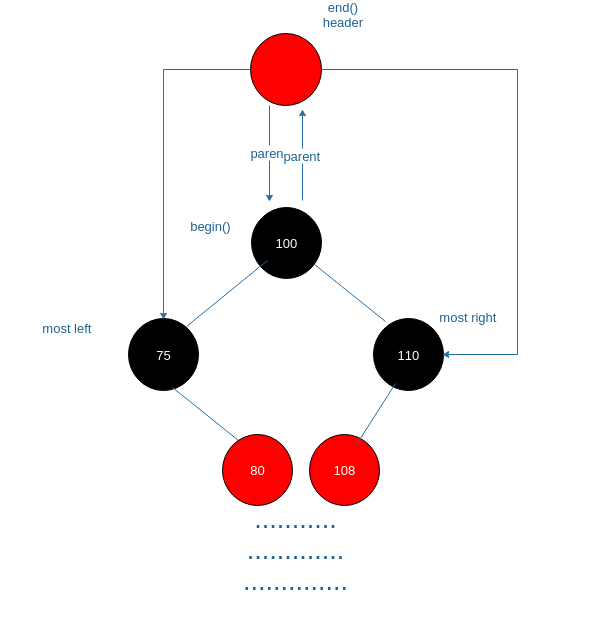。
|
||
图中省略号表示节点没有画完,还有其他节点,所以省略。
|
||
|
||
## 1.红黑树节点基类
|
||
|
||
红黑树基类,非常简单,在文件开头定义了颜色标记。
|
||
|
||
基类中包含了指向自己的指针,分别定义了left、right、parent,同时包含了一个颜色标记常量,而里面有两个核心函数,目的是获取红黑树中最小节点与最大节点。
|
||
我们知道对于二分搜索树获取最小节点就是左子树一直往下搜,最大节点就是右子树一直往下搜即可。
|
||
|
||
```cpp
|
||
// 颜色标记
|
||
enum _Rb_tree_color { _S_red = false, _S_black = true };
|
||
|
||
// 基类
|
||
struct _Rb_tree_node_base
|
||
{
|
||
// typedef重命名
|
||
typedef _Rb_tree_node_base* _Base_ptr;
|
||
|
||
// 颜色
|
||
_Rb_tree_color _M_color;
|
||
// 指向父亲
|
||
_Base_ptr _M_parent;
|
||
// 指向左孩子
|
||
_Base_ptr _M_left;
|
||
// 指向右孩子
|
||
_Base_ptr _M_right;
|
||
|
||
// 求红黑树的最小节点
|
||
static _Base_ptr
|
||
_S_minimum(_Base_ptr __x) _GLIBCXX_NOEXCEPT
|
||
{
|
||
while (__x->_M_left != 0) __x = __x->_M_left;
|
||
return __x;
|
||
}
|
||
|
||
// 求红黑树最大节点
|
||
static _Base_ptr
|
||
_S_maximum(_Base_ptr __x) _GLIBCXX_NOEXCEPT
|
||
{
|
||
while (__x->_M_right != 0) __x = __x->_M_right;
|
||
return __x;
|
||
}
|
||
|
||
};
|
||
|
||
```
|
||
## 2.红黑树节点
|
||
|
||
红黑树节点继承自红黑树基类。
|
||
```cpp
|
||
template<typename _Val>
|
||
struct _Rb_tree_node : public _Rb_tree_node_base
|
||
{
|
||
typedef _Rb_tree_node<_Value>* _Link_type;//节点指针,指向数据节点
|
||
_Value _M_value_field;//节点数据域,即关键字
|
||
};
|
||
```
|
||
|
||
## 3.红黑树迭代器
|
||
|
||
红黑树迭代器里面有一个红黑树基类成员,然后通过该成员进行迭代器的相关操作。
|
||
同时,我们可以知道该迭代器属于`bidirectional_iterator_tag`。
|
||
|
||
里面也包含了萃取机相关需要的typedef。
|
||
|
||
```cpp
|
||
template<typename _Tp>
|
||
struct _Rb_tree_iterator
|
||
{
|
||
typedef _Tp value_type;
|
||
typedef _Tp& reference;
|
||
typedef _Tp* pointer;
|
||
|
||
typedef bidirectional_iterator_tag iterator_category;
|
||
typedef ptrdiff_t difference_type;
|
||
|
||
typedef _Rb_tree_iterator<_Tp> _Self;
|
||
typedef _Rb_tree_node_base::_Base_ptr _Base_ptr;
|
||
typedef _Rb_tree_node<_Tp>* _Link_type;
|
||
|
||
_Base_ptr _M_node;
|
||
};
|
||
|
||
```
|
||
|
||
获取数据
|
||
|
||
|
||
```cpp
|
||
reference
|
||
operator*() const _GLIBCXX_NOEXCEPT
|
||
{ return *static_cast<_Link_type>(_M_node)->_M_valptr(); }
|
||
|
||
pointer
|
||
operator->() const _GLIBCXX_NOEXCEPT
|
||
{ return static_cast<_Link_type> (_M_node)->_M_valptr(); }
|
||
|
||
```
|
||
|
||
重载++操作符
|
||
|
||
```cpp
|
||
_Self&
|
||
operator++() _GLIBCXX_NOEXCEPT
|
||
{
|
||
_M_node = _Rb_tree_increment(_M_node);
|
||
return *this;
|
||
}
|
||
```
|
||
而`_Rb_tree_increment`底层是`local_Rb_tree_increment`,如下实现:
|
||
|
||
```cpp
|
||
static _Rb_tree_node_base *
|
||
local_Rb_tree_increment( _Rb_tree_node_base* __x ) throw ()
|
||
{
|
||
if ( __x->_M_right != 0 ) /* 存在右子树,那么下一个节点为右子树的最小节点 */
|
||
{
|
||
__x = __x->_M_right;
|
||
while ( __x->_M_left != 0 )
|
||
__x = __x->_M_left;
|
||
}else {
|
||
/* 不存在右子树,那么分为两种情况:自底往上搜索,当前节点为父节点的左孩子的时候,父节点就是后继节点; */
|
||
/* 第二种情况:_x为header节点了,那么_x就是最后的后继节点. 简言之_x为最小节点且往上回溯,一直为父节点的右孩子,直到_x变为父节点,_y为其右孩子 */
|
||
_Rb_tree_node_base *__y = __x->_M_parent;
|
||
while ( __x == __y->_M_right )
|
||
{
|
||
__x = __y;
|
||
__y = __y->_M_parent;
|
||
}
|
||
if ( __x->_M_right != __y )
|
||
__x = __y;
|
||
}
|
||
return (__x);
|
||
}
|
||
```
|
||
重载--操作符:
|
||
|
||
|
||
```cpp
|
||
_Self&
|
||
operator--() _GLIBCXX_NOEXCEPT
|
||
{
|
||
_M_node = _Rb_tree_decrement(_M_node);
|
||
return *this;
|
||
}
|
||
```
|
||
同理,而`_Rb_tree_decrement`底层是`local_Rb_tree_decrement`,如下实现:
|
||
|
||
```cpp
|
||
static _Rb_tree_node_base *
|
||
local_Rb_tree_decrement( _Rb_tree_node_base * __x )
|
||
throw ()
|
||
{
|
||
/* header节点 */
|
||
if ( __x->_M_color ==
|
||
_S_red
|
||
&& __x
|
||
->_M_parent->_M_parent == __x )
|
||
__x = __x->_M_right;
|
||
else if ( __x->_M_left != 0 ) /* 左节点不为空,返回左子树中最大的节点 */
|
||
{
|
||
_Rb_tree_node_base *__y = __x->_M_left;
|
||
while ( __y->_M_right != 0 )
|
||
__y = __y->_M_right;
|
||
__x = __y;
|
||
}else {
|
||
/* 自底向上找到当前节点为其父节点的右孩子,那么父节点就是前驱节点 */
|
||
_Rb_tree_node_base *__y = __x->_M_parent;
|
||
while ( __x == __y->_M_left )
|
||
{
|
||
__x = __y;
|
||
__y = __y->_M_parent;
|
||
}
|
||
__x = __y;
|
||
}
|
||
return
|
||
(__x);
|
||
}
|
||
```
|
||
|
||
|
||
重载==与!=操作符,直接判断节点指针是否相等。
|
||
|
||
```cpp
|
||
bool
|
||
operator==(const _Self& __x) const _GLIBCXX_NOEXCEPT
|
||
{ return _M_node == __x._M_node; }
|
||
|
||
bool
|
||
operator!=(const _Self& __x) const _GLIBCXX_NOEXCEPT
|
||
{ return _M_node != __x._M_node; }
|
||
|
||
```
|
||
|
||
|
||
|
||
其他重要函数,黑节点统计:
|
||
|
||
```cpp
|
||
unsigned int
|
||
_Rb_tree_black_count(const _Rb_tree_node_base *__node,
|
||
const _Rb_tree_node_base *__root) throw() {
|
||
if (__node == 0)
|
||
return 0;
|
||
unsigned int __sum = 0;
|
||
do {
|
||
if (__node->_M_color == _S_black)
|
||
++__sum;
|
||
if (__node == __root)
|
||
break;
|
||
__node = __node->_M_parent;
|
||
} while (1);
|
||
return __sum;
|
||
}
|
||
```
|
||
后面来阐述最重要的插入操作。
|
||
|
||
## 4.红黑树操作
|
||
|
||
比较重要的是,里面使用节点基类来声明了一个指针。还包含了一个`_Rb_tree_impl`用来对红黑树初始化操作与内存管理操作。里面还包含了两种迭代器,一个rbtree,另一个是reverse,说明支持rbegin,rend操作。
|
||
```cpp
|
||
template<typename _Key, typename _Val, typename _KeyOfValue,
|
||
typename _Compare, typename _Alloc = allocator<_Val> >
|
||
class _Rb_tree
|
||
{
|
||
|
||
protected:
|
||
typedef _Rb_tree_node_base* _Base_ptr;
|
||
|
||
template<typename _Key_compare,
|
||
bool _Is_pod_comparator = __is_pod(_Key_compare)>
|
||
struct _Rb_tree_impl : public _Node_allocator
|
||
{
|
||
_Key_compare _M_key_compare;
|
||
_Rb_tree_node_base _M_header;
|
||
size_type _M_node_count; // Keeps track of size of tree.
|
||
|
||
_Rb_tree_impl()
|
||
: _Node_allocator(), _M_key_compare(), _M_header(),
|
||
_M_node_count(0)
|
||
{ _M_initialize(); }
|
||
|
||
_Rb_tree_impl(const _Key_compare& __comp, const _Node_allocator& __a)
|
||
: _Node_allocator(__a), _M_key_compare(__comp), _M_header(),
|
||
_M_node_count(0)
|
||
{ _M_initialize(); }
|
||
|
||
private:
|
||
void
|
||
_M_initialize()
|
||
{
|
||
this->_M_header._M_color = _S_red;
|
||
this->_M_header._M_parent = 0;
|
||
this->_M_header._M_left = &this->_M_header;
|
||
this->_M_header._M_right = &this->_M_header;
|
||
}
|
||
|
||
};
|
||
public:
|
||
typedef _Rb_tree_iterator<value_type> iterator;
|
||
typedef std::reverse_iterator<iterator> reverse_iterator;
|
||
private:
|
||
_Rb_tree_impl<_Compare> _M_impl;
|
||
};
|
||
```
|
||
> 获取红黑树根节点、最左与最右节点
|
||
|
||
回到一开始的图:
|
||
。
|
||
|
||
|
||
```cpp
|
||
// 图中100 节点
|
||
_Base_ptr&
|
||
_M_root() _GLIBCXX_NOEXCEPT
|
||
{ return this->_M_impl._M_header._M_parent; }
|
||
|
||
// 图中most left标记
|
||
_Base_ptr&
|
||
_M_leftmost() _GLIBCXX_NOEXCEPT
|
||
{ return this->_M_impl._M_header._M_left; }
|
||
|
||
|
||
// 图中most right标记
|
||
_Base_ptr&
|
||
_M_rightmost() _GLIBCXX_NOEXCEPT
|
||
{ return this->_M_impl._M_header._M_right; }
|
||
_Link_type
|
||
|
||
// 图中begin()标记
|
||
_M_begin() _GLIBCXX_NOEXCEPT
|
||
{ return static_cast<_Link_type>(this->_M_impl._M_header._M_parent); }
|
||
|
||
// 图中end()标记
|
||
_Link_type
|
||
_M_end() _GLIBCXX_NOEXCEPT
|
||
{ return reinterpret_cast<_Link_type>(&this->_M_impl._M_header); }
|
||
|
||
```
|
||
我们再看代码是不是非常清晰!
|
||
|
||
|
||
|
||
|
||
## 5.红黑树插入
|
||
|
||
|
||
|
||
### 5.1 旋转过程
|
||
|
||
左旋转是将该节点的右节点设置为它的父节点,该节点将变成刚才右节点的左孩子
|
||
|
||
直接看源码中的图与代码对比即可。
|
||
|
||
在`tree.cc`源码中实现函数为`local_Rb_tree_rotate_left`与`local_Rb_tree_rotate_right`。
|
||
下面我们将源码进行剖析成比较容易理解的代码,具体见注释。
|
||
大家会发现函数名与变量名与源码不同,是因为下面是当时自己实现的,但是不影响源码阅读,就直接拿来对比了。
|
||
|
||
```cpp
|
||
/**
|
||
* 当前节点的左旋转过程
|
||
* 将该节点的右节点设置为它的父节点,该节点将变成刚才右节点的左孩子
|
||
* @param _x
|
||
*/
|
||
// _x _y
|
||
// / \ 左旋转 / \
|
||
// T1 _y ---------> _x T3
|
||
// / \ / \
|
||
// T2 T3 T1 T2
|
||
void leftRotate(Node *_x) {
|
||
// step1 处理_x的右孩子
|
||
// 右节点变为_x节点的父亲节点,先保存一下右节点
|
||
Node *_y = _x->right;
|
||
// T2变为node的右节点
|
||
_x->right = _y->left;
|
||
if (NULL != _y->left)
|
||
_y->left->parent = _x;
|
||
|
||
// step2 处理_y与父亲节点关系
|
||
_y->parent = _x->parent; // 原来_x的父亲变为_y的父亲
|
||
// 说明原来_x为root节点,此时需要将_y设为新root节点
|
||
// 或者判断NULL == _y->parent
|
||
if (_x == root)
|
||
root = _y;
|
||
else if (_x == _x->parent->left) // 原_x的父节点的左孩子连接新节点_y
|
||
_x->parent->left = _y;
|
||
else // 原_x的父节点的右孩子连接新节点_y
|
||
_x->parent->right = _y;
|
||
|
||
// step3 处理_x与_y关系
|
||
_y->left = _x; // _y的左孩子为_x
|
||
_x->parent = _y; // _x的父亲是_y
|
||
}
|
||
```
|
||
|
||
同理,右旋转如下:
|
||
```cpp
|
||
// _x _y
|
||
// / \ 右旋转 / \
|
||
// _y T2 -------------> T0 _x
|
||
// / \ / \
|
||
// T0 T1 T1 T2
|
||
void rightRotate(Node *_x) {
|
||
// step1 处理_x的左孩子
|
||
// 左节点变为_x节点的父亲节点,先保存一下左节点
|
||
Node *_y = _x->left;
|
||
// T1变为_x的左孩子
|
||
_x->left = _y->right;
|
||
if (NULL != _y->right)
|
||
_y->right->parent = _x;
|
||
|
||
// step2 处理_y与父节点之间的关系
|
||
// 或者判断_x->parent==NULL
|
||
if (_x == root)
|
||
root = _y;
|
||
else if (_x == _x->parent->right)
|
||
_x->parent->right = _y;
|
||
else
|
||
_x->parent->left = _y;
|
||
|
||
// step3 处理_x与_y关系
|
||
_y->right = _x; // _y的右孩子为_x
|
||
_x->parent = _y; // _x的父亲是_y
|
||
}
|
||
```
|
||
|
||
|
||
case 1.1: 父节点为红色且其叔叔节点也为红色,则将父亲、叔叔置为黑色,祖父置为红色。
|
||
|
||
|
||
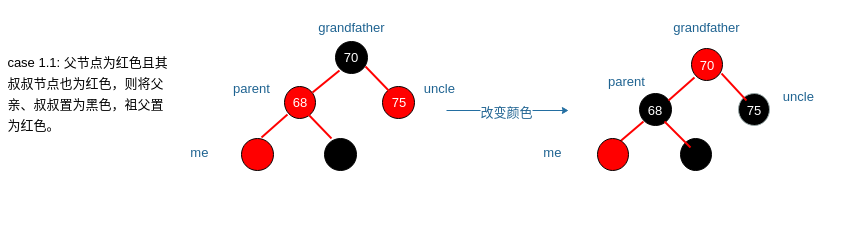
|
||
|
||
case 1.2 若无叔叔节点或者其叔叔节点为黑色分为下面两种:
|
||
|
||
情况1.2.1:x的叔叔节点y是黑色且x是一个右孩子
|
||
|
||
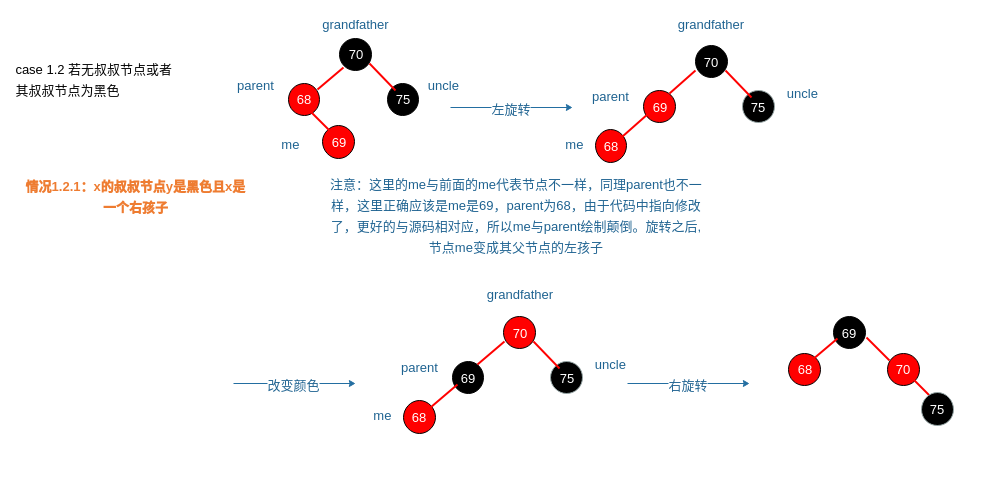
|
||
|
||
情况1.2.2:x的叔叔节点y是黑色且x是一个左孩子
|
||
|
||
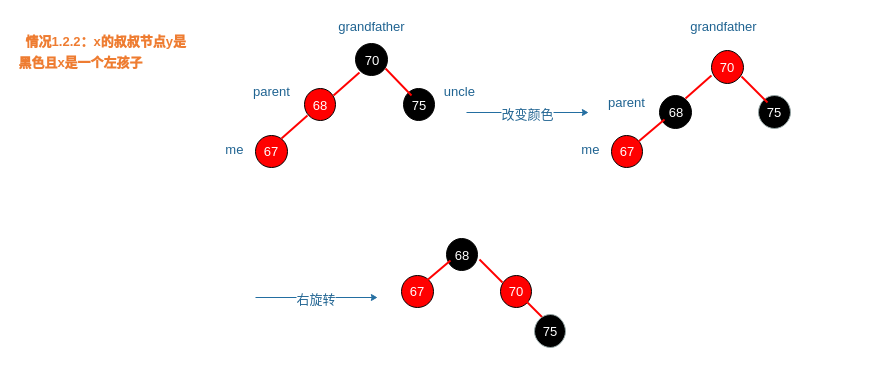
|
||
|
||
对应源代码中:
|
||
```cpp
|
||
_Rb_tree_node_base *const __y = __xpp->_M_right; // 得到叔叔节点
|
||
if (__y && __y->_M_color == _S_red) // case1: 叔叔节点存在,且为红色
|
||
{
|
||
/**
|
||
* 解决办法是:颜色翻转,父亲与叔叔的颜色都变为黑色,祖父节点变为红色,然后当前节点设为祖父,依次网上来判断是否破坏了红黑树性质
|
||
*/
|
||
__x->_M_parent->_M_color = _S_black; // 将其父节点改为黑色
|
||
__y->_M_color = _S_black; // 将其叔叔节点改为黑色
|
||
__xpp->_M_color = _S_red; // 将其祖父节点改为红色
|
||
__x = __xpp; // 修改_x,往上回溯
|
||
} else { // 无叔叔或者叔叔为黑色
|
||
if (__x == __x->_M_parent->_M_right) { // 当前节点为父亲节点的右孩子
|
||
__x = __x->_M_parent;
|
||
local_Rb_tree_rotate_left(__x, __root); // 以父节点进行左旋转
|
||
}
|
||
// 旋转之后,节点x变成其父节点的左孩子
|
||
__x->_M_parent->_M_color = _S_black; // 将其父亲节点改为黑色
|
||
__xpp->_M_color = _S_red; // 将其祖父节点改为红色
|
||
local_Rb_tree_rotate_right(__xpp, __root); // 以祖父节点右旋转
|
||
}
|
||
|
||
```
|
||
|
||
另外一个是上述对称过程:
|
||
|
||
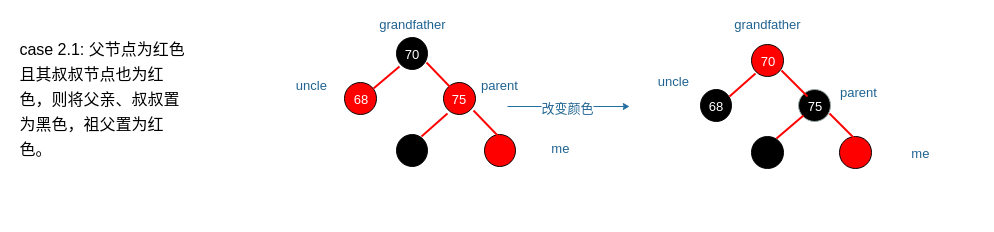
case 2.1: 父节点为红色且其叔叔节点也为红色,则将父亲、叔叔置为黑色,祖父置为红色。
|
||
|
||
|
||
|
||
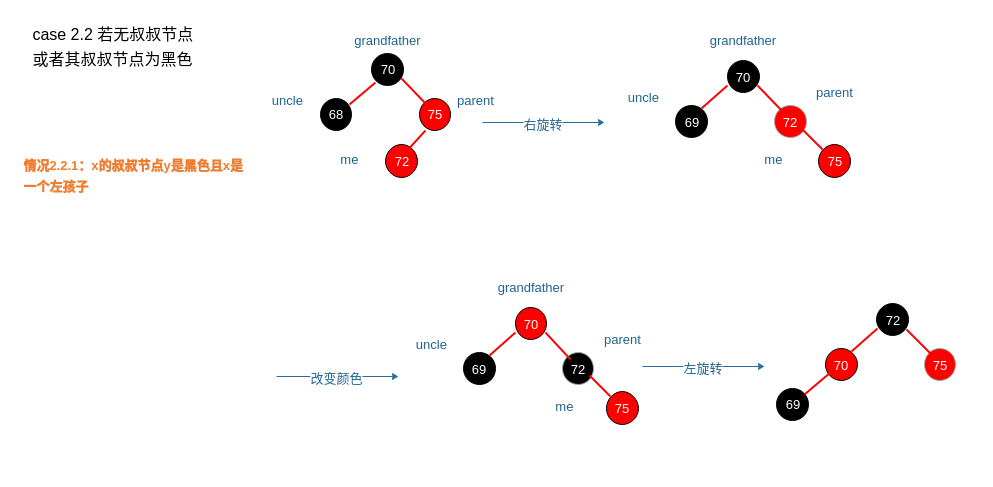
case 2.2 若无叔叔节点或者其叔叔节点为黑色
|
||
|
||
|
||
|
||
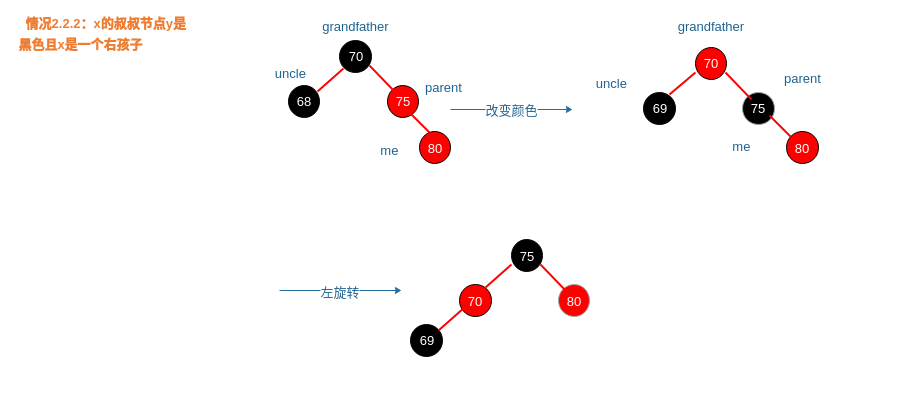
情况2.2.1:x的叔叔节点y是黑色且x是一个左孩子
|
||
|
||
|
||
|
||
|
||
|
||
|
||
```cpp
|
||
_Rb_tree_node_base *const __y = __xpp->_M_left; // 保存叔叔节点
|
||
if (__y && __y->_M_color == _S_red) { // 叔叔节点存在且为红色
|
||
__x->_M_parent->_M_color = _S_black; // 父亲节点改为黑色
|
||
__y->_M_color = _S_black; // 祖父节点改为红色
|
||
__xpp->_M_color = _S_red;
|
||
__x = __xpp;
|
||
} else { // 若无叔叔节点或者其叔叔节点为黑色
|
||
if (__x == __x->_M_parent->_M_left) { // 当前节点为父亲节点的左孩子
|
||
__x = __x->_M_parent;
|
||
local_Rb_tree_rotate_right(__x, __root); // 以父节点右旋转
|
||
}
|
||
__x->_M_parent->_M_color = _S_black; // 父节点置为黑色
|
||
__xpp->_M_color = _S_red; // 祖父节点置为红色
|
||
local_Rb_tree_rotate_left(__xpp, __root); // 左旋转
|
||
}
|
||
|
||
```
|
||
|
||
|
||
|
||
`_Rb_tree_insert_and_rebalance`完整解析:
|
||
|
||
```cpp
|
||
void
|
||
_Rb_tree_insert_and_rebalance(const bool __insert_left,
|
||
_Rb_tree_node_base *__x,
|
||
_Rb_tree_node_base *__p,
|
||
_Rb_tree_node_base &__header) throw() {
|
||
_Rb_tree_node_base * &__root = __header._M_parent;
|
||
|
||
// Initialize fields in new node to insert.
|
||
__x->_M_parent = __p;
|
||
__x->_M_left = 0;
|
||
__x->_M_right = 0;
|
||
__x->_M_color = _S_red;
|
||
|
||
// 处理__header部分
|
||
// Insert.
|
||
// Make new node child of parent and maintain root, leftmost and
|
||
// rightmost nodes.
|
||
// N.B. First node is always inserted left.
|
||
if (__insert_left) {
|
||
__p->_M_left = __x; // also makes leftmost = __x when __p == &__header
|
||
|
||
if (__p == &__header) {
|
||
__header._M_parent = __x;
|
||
__header._M_right = __x;
|
||
} else if (__p == __header._M_left)
|
||
__header._M_left = __x; // maintain leftmost pointing to min node
|
||
} else {
|
||
__p->_M_right = __x;
|
||
|
||
if (__p == __header._M_right)
|
||
__header._M_right = __x; // maintain rightmost pointing to max node
|
||
}
|
||
|
||
// Rebalance.
|
||
while (__x != __root
|
||
&& __x->_M_parent->_M_color == _S_red) // 若新插入节点不是为RB-Tree的根节点,且其父节点color属性也是红色,即违反了性质4.
|
||
{
|
||
_Rb_tree_node_base *const __xpp = __x->_M_parent->_M_parent; // 祖父节点
|
||
|
||
if (__x->_M_parent == __xpp->_M_left) // 父亲是祖父节点的左孩子
|
||
{
|
||
_Rb_tree_node_base *const __y = __xpp->_M_right; // 得到叔叔节点
|
||
if (__y && __y->_M_color == _S_red) // case1: 叔叔节点存在,且为红色
|
||
{
|
||
/**
|
||
* 解决办法是:颜色翻转,父亲与叔叔的颜色都变为黑色,祖父节点变为红色,然后当前节点设为祖父,依次网上来判断是否破坏了红黑树性质
|
||
*/
|
||
__x->_M_parent->_M_color = _S_black; // 将其父节点改为黑色
|
||
__y->_M_color = _S_black; // 将其叔叔节点改为黑色
|
||
__xpp->_M_color = _S_red; // 将其祖父节点改为红色
|
||
__x = __xpp; // 修改_x,往上回溯
|
||
} else { // 无叔叔或者叔叔为黑色
|
||
if (__x == __x->_M_parent->_M_right) { // 当前节点为父亲节点的右孩子
|
||
__x = __x->_M_parent;
|
||
local_Rb_tree_rotate_left(__x, __root); // 以父节点进行左旋转
|
||
}
|
||
// 旋转之后,节点x变成其父节点的左孩子
|
||
__x->_M_parent->_M_color = _S_black; // 将其父亲节点改为黑色
|
||
__xpp->_M_color = _S_red; // 将其祖父节点改为红色
|
||
local_Rb_tree_rotate_right(__xpp, __root); // 以祖父节点右旋转
|
||
}
|
||
} else { // 父亲是祖父节点的右孩子
|
||
_Rb_tree_node_base *const __y = __xpp->_M_left; // 保存叔叔节点
|
||
if (__y && __y->_M_color == _S_red) { // 叔叔节点存在且为红色
|
||
__x->_M_parent->_M_color = _S_black; // 父亲节点改为黑色
|
||
__y->_M_color = _S_black; // 祖父节点改为红色
|
||
__xpp->_M_color = _S_red;
|
||
__x = __xpp;
|
||
} else { // 若无叔叔节点或者其叔叔节点为黑色
|
||
if (__x == __x->_M_parent->_M_left) { // 当前节点为父亲节点的左孩子
|
||
__x = __x->_M_parent;
|
||
local_Rb_tree_rotate_right(__x, __root); // 以父节点右旋转
|
||
}
|
||
__x->_M_parent->_M_color = _S_black; // 父节点置为黑色
|
||
__xpp->_M_color = _S_red; // 祖父节点置为红色
|
||
local_Rb_tree_rotate_left(__xpp, __root); // 左旋转
|
||
}
|
||
}
|
||
}
|
||
//若新插入节点为根节点,则违反性质2
|
||
//只需将其重新赋值为黑色即可
|
||
__root->_M_color = _S_black;
|
||
}
|
||
```
|
||
|
||
## 5.2插入总结
|
||
|
||
根据上述插入过程与源码分析,我们得出下面三种:
|
||
假设P代码父亲节点,N代表当前新插入节点,U代表叔叔节点,G代表祖父节点。
|
||
|
||
|
||
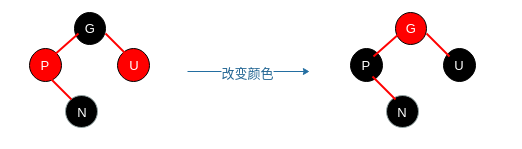
case 1:U为红色,P、N也都为红色,则可以通过改变颜色,自底向上递归调整,下次N就变味G,往上判断即可。如果碰巧将根节点染成了红色, 可以在算法的最后强制root改为黑。
|
||
|
||
|
||
|
||
case 2:U为黑色,考虑N是P的左孩子还是右孩子。
|
||
|
||
case2.1 如果是右孩子,先进行左旋转,再进入下一种情况。
|
||
|
||
|
||

|
||
|
||
case2.2 可能是上述情况变化而来,但不一定是!策略为:右旋转,改变颜色。
|
||
|
||
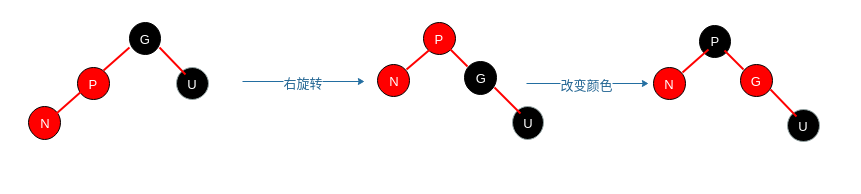
|
||
|
||
|
||
经过上述源码的分析得知,红黑树插入为镜像变换,另一种情况刚好相反。
|
||
|
||
|
||
删除操作,比较复杂,这里就暂时没分析了,后面补上。。。
|
||
|
||
|
||
|
||
## 6.使用
|
||
|
||
前面说了那么多,如何使用呢?
|
||
|
||
引入头文件:
|
||
```
|
||
#include<map>或者<set>
|
||
```
|
||
类定义:
|
||
```
|
||
_Rb_tree<int, int, _Identity<int>, less<int>> itree;
|
||
```
|
||
然后调用相应函数即可。
|